


华中科技大学附属中学优秀青年数学教师万兵
荆楚网消息(记者 陈敏 通讯员 郭海军)6月21日,2016年武汉市中考结束。荆楚网独家邀请华中科技大学附属中学优秀青年数学教师万兵老师点评2016年武汉市中考数学试题。
2016年武汉市中考数学试题给万兵老师的第一感觉是:“这是一份简洁亲和,回归数学本味的试题,看似波澜不惊,实则连绵起伏。”万兵老师说,在形式上,它延续了今年元月调考、四月调考的命题风格,难度较去年中考略有降低,考试结束后,不少考生神色轻松,表示很多题目有似曾相识之感,理解起来也比较顺畅,缓解了他们在心态上的恐惧和不安,总体上看,有效的发挥了自己的真实水平。
仔细揣度这份试卷,会发现试卷的整体布局和考点与往年相比保持了一定的延续性和稳定性,着重考察学生对基础知识的理解与掌握,涉及面广,如:无理数范围的估算、分式有意义的条件、乘法公式、概率统计、与图形变换相关的坐标运算、三视图、科学计数法、一步概率、平行与折叠、一元一次方程的解法、全等三角形的证明、概率统计中数据的分析与处理等,学生能比较轻松的驾驭;同时,对学生的思维发散与迁移能力也提出了较高的要求,如选择题的第9题,考察与圆相关的动点轨迹问题;第10题考察等腰三角形的存在性问题。填空题第15题考察对动态复合函数的理解和图像分析、16题考察勾股定理及其逆定理,并与常见的“K字型”相似相结合。解答题第21题是圆的证明与计算问题中较为常见的模型,辅助线的添加比较常规,但相关边长的计算存有障碍,第22题,虽是老生常谈的销售利润问题,但问题的呈现方式有所创新,关键是要读懂题意,完成二次函数的建模,第23题逐级铺垫,引导学生拾级而上,在熟悉基本相似模型的同时,还要具备较强的化归能力,将未知的问题转化为熟知的模型,第24题第(2)问要求学生思维严谨,面对无图问题,注意分类讨论,第(3)问则对学生计算能力、技巧和数学思想要求更高。这么一份看似传统的试卷背后,却蕴藏着对数学火热的思考,有效的区分了不同层级的学生,具备较好的选拔功能。
结合试卷中的具体问题,万兵老师从以下三个方面分析了本套试卷的亮点:
1、在传统和创新之间,选择了融合
“传统与创新”是一个老话题,但永远是事物发展的一个新课题,任何一个创新,不能是无本之木,无源之水。
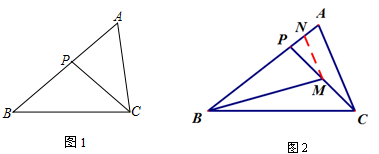
第23题是几何综合题,在我们的传统印象里,本题方法灵活多变,推理性强,时常让人感觉难以入手,但本题删繁就简,题干清晰简洁,从学生熟知的“母子型”(图1)相似出发,试图去解决图(2)中线段BP的长度问题,这么一个看似摸不着头脑的问题,在巧妙地借助中位线MN后,构造出了一对新的“母子型”相似,建立方程,使问题有效地得以解决。这种重思想,减轻考生繁杂几何推理负担的考察方式使考察重心更为明确,显得更为清新明快,这其中既有传统的坚守,又有创新的突破,凸显能力立意,值得细细品味。
2、在直观与抽象之间,寻找了平衡
从元月调考和四月调考的趋势上来看,二次函数图像与动直线的交点问题是热点,这种考察的趋势意在更好的实现初高中的衔接与融合,但对学生数形结合的能力要求颇高,且抽象性强。本次考试,将该思想渗透在了填空题的第15题,在经典与时尚之间,寻求到了平衡。如:对于函数y=|2x+b|的图像,涉及复合函数的图像问题,若生硬给出,会给不少学生设下障碍,致使无从下手,但题干人性化的解读让考生能更直观的了解函数y=|2x+b|的图像,豁然开朗,即将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象,学生在这种具象的情境之下,更容易解决问题。
3、在知识和方法之中,锤炼了思维
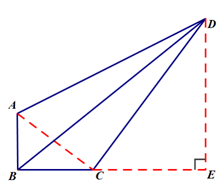
武汉市中考命题指导思想强调学生要在丰富的数学活动过程中,激烈的思维碰撞中,帮助学生获取知识和技能,从而提升他们的数学思考能力。本次试卷的第16题具有较好的导向性,对知识和方法的渗透自然、流畅、符合学生的学习能力和实情,同时对学生思维的灵活性也提出了较高的要求。本题中,学生需要有敏锐的数据处理能力,利用AB=3,BC=4得到AC=5,发现,利用勾股定理逆定理得到,再构造出K字型相似,即△ABC∽△CED,算得:DE=8,CE=6,从而在Rt△BDE中,求得BD的长。本题不偏不怪甚至不难,但对学生的考察甚是全面,既有数据的处理和分析,又有常见相似型的构造,亲和而大气,锤炼了学生的思维。
万兵老师告诉记者,整张试卷给我们一个重要的启示:不论是教师,还是学生,都要从浩瀚的题海中解脱出来,重视基础知识、培养基本技能,真正做到回归教材,回归课堂,回归到知识的本源中去,回归到我们的数学文化中去。
名师简介:万兵,华中科技大学附属中学优秀青年数学教师,东湖高新区优质课竞赛二等奖获得者。
(作者: 编辑:)